控件的布局
本文共 2392 字,大约阅读时间需要 7 分钟。
控 件 的 布 局 控件的布局 控件的布局
1.控件的布局
控件的布局:当窗口中有多个控件时,如何决定每个控件的位置和大小。
布局的方式:
1 可视化布局:在设计器里拖放操作2 手工布局:用代码计算每个控件的位置3 使用布局器:用布局器自动布局
演示:添加几个控件,进行可视化布局
按钮, Button文本框,TextBox图片框,PictureBox
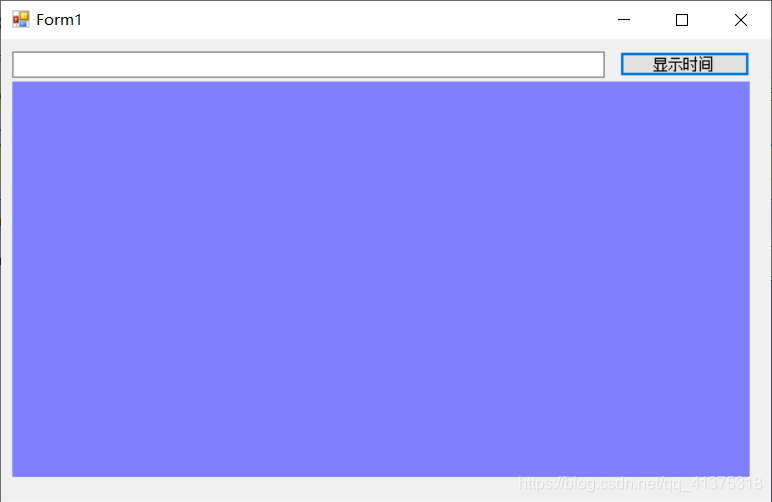
当窗口改变大小时,布局并不能够自动适应所以,此种布局只适用于窗口大小固定不变的情况
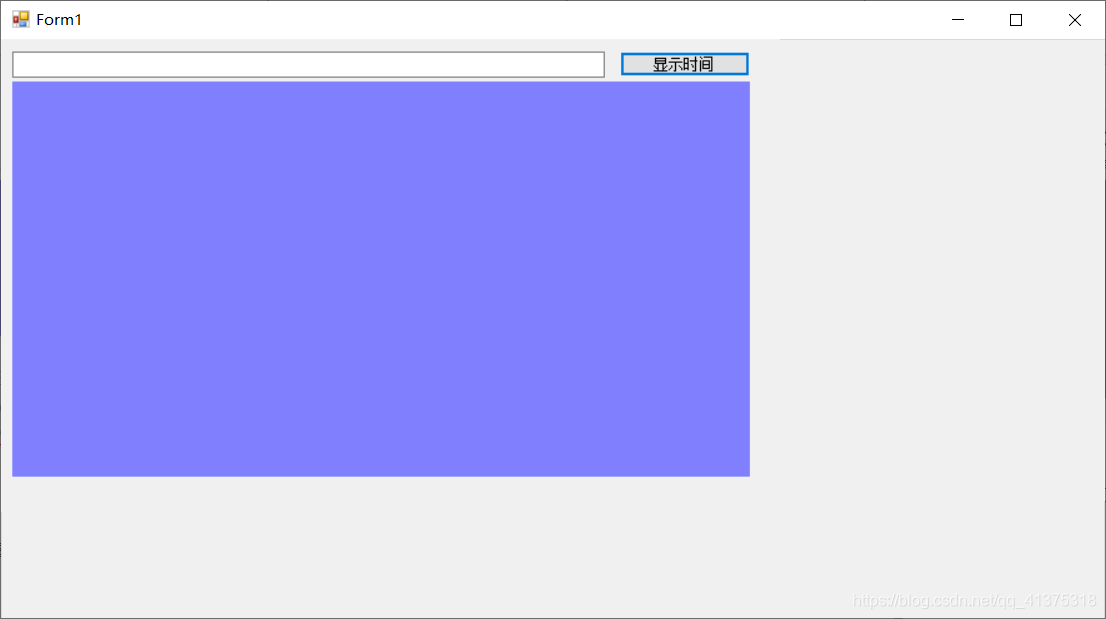
2.手工布局
手工布局:用代码计算每个控件的位置
重写OnIayout方法override void OnLayout (LayoutEventArgs levent){ } 当窗口大小改变时,会自动调用这个方法重新布局
演示:在窗口中添加几个控件,并实现手工布局。
其中,窗口的大小: Size:窗口大小(含标题栏和边框) ClientSize :仅窗口客户区的大小using System;using System.Collections.Generic;using System.ComponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Threading.Tasks;using System.Windows.Forms;namespace WinForm基础3{ public partial class Form1 : Form { public Form1() { InitializeComponent(); this.timeField.AutoSize = false; } protected override void OnLayout(LayoutEventArgs levent) { // 1.调用父类的OnLayout(),不是必需的 base.OnLayout(levent); // 2.获取窗口的大小ClientSize(仅客户区,不含标题栏) int w = this.ClientSize.Width; int h = this.ClientSize.Height; // 3.计算每个控件的位置和大小 int yoff = 0; yoff = 4; this.timeField.Location = new Point(0, yoff); this.timeField.Size = new Size(w - 80, 30); this.button1.Location = new Point(w - 80, yoff); this.button1.Size = new Size(80, 30); yoff += 30; yoff += 4; this.pictureBox1.Location = new Point(0, yoff); this.pictureBox1.Size = new Size(w, h - yoff - 4); } private void On_Test(object sender, EventArgs e) { string timeStr = DateTime.Now.ToString("yyyy-MM-dd HH:mm:ss"); timeField.Text = timeStr; } }} 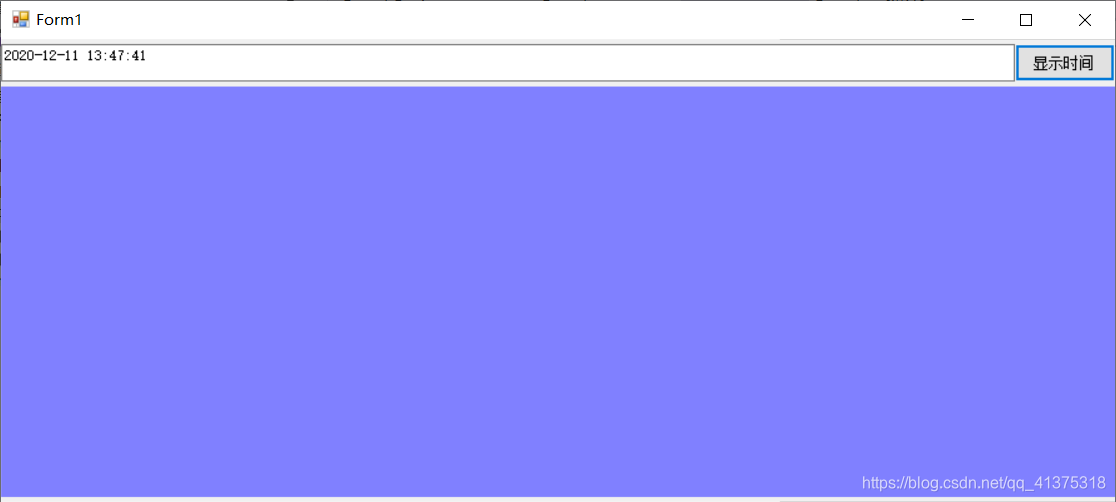
1 TextBox : AutoSize = false
否则它会自己计算所需的大小2区分窗口的Size和 ClientSize
3窗口的自适应:当窗口大小变化时,会自动调用OnLayout()方法
3.Anchor
控件的两个通用的布局属性:
Anchor:锚定,将控件固定于某个位置Dock:停靠,将控件停靠在一侧或中央
演示:设置一个控件的 Anchor为Top l Right
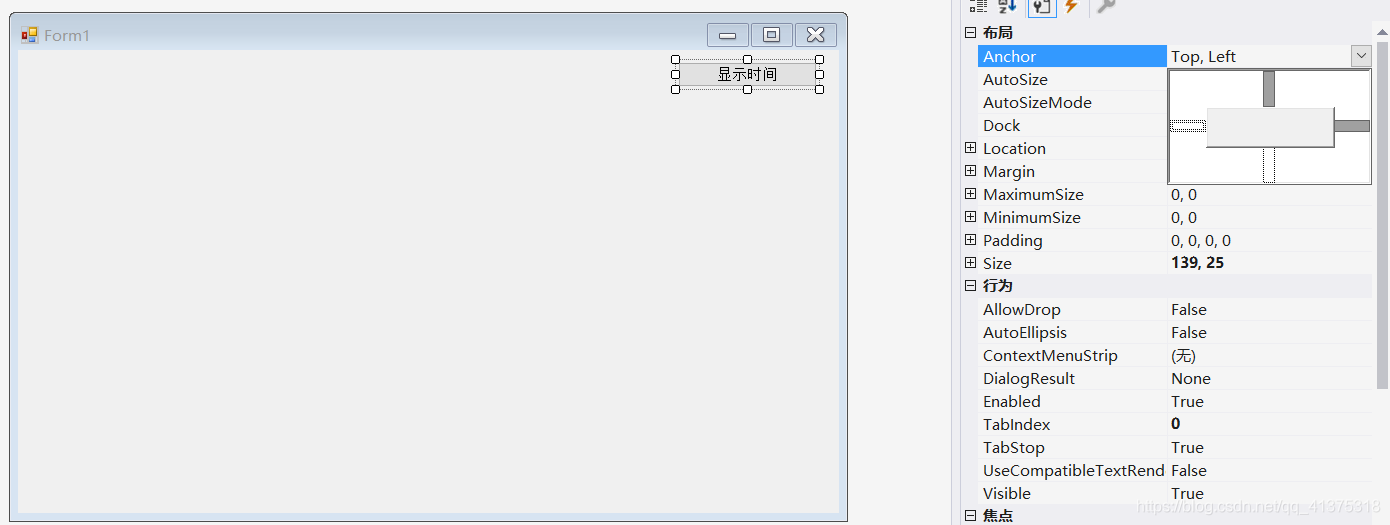
 1 锚定于左下角
1 锚定于左下角 - Anchor =Left | Bottom
2 锚定于右下角
- Anchor = Right | Bottom
3锚定于上边缘、水平拉伸
- Anchor = Top l Left l Right
4锚定于上边缘、水平居中-水平居中
- Anchor =Top l Left l Right
5拉伸
- Anchor = Top l Right I Bottom l Left
6居中
- 水平居中,垂直居中-Anchor: None
4.Dock
Dock:停靠,将控件停靠在一侧或中央
上 Top下 Bottom左 Left右 Right中 Fill无 None
演示:Panel,面板
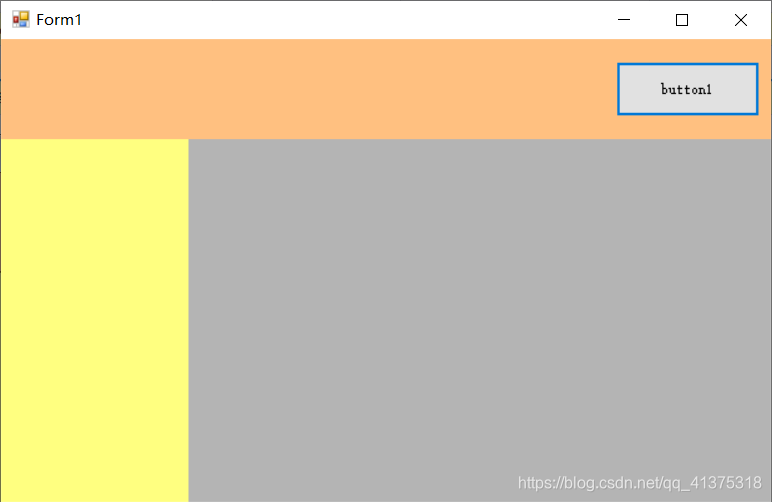
1添加一个Panel,停靠在上侧2添加一个Panel,依靠在左侧3添加一个PictureBox,依靠在中央
依靠于左右两侧时,可以调整宽度;上下两侧时,可以调整高度。
转载地址:http://pzdtz.baihongyu.com/
你可能感兴趣的文章
MySQL数据库与Informix:能否创建同名表?
查看>>
mysql自增id超大问题查询
查看>>
MySQL锁与脏读、不可重复读、幻读详解
查看>>
MySQL集群解决方案(4):负载均衡
查看>>
mysql颠覆实战笔记(八)--mysql的自定义异常处理怎么破
查看>>
MySQL高级-MySQL并发参数调整
查看>>
MySQL高级-视图
查看>>
MySQL:判断逗号分隔的字符串中是否包含某个字符串
查看>>
Nacos在双击startup.cmd启动时提示:Unable to start embedded Tomcat
查看>>
Nacos安装教程(非常详细)从零基础入门到精通,看完这一篇就够了
查看>>
Nacos配置中心集群原理及源码分析
查看>>
nacos配置自动刷新源码解析
查看>>
Nacos集群搭建
查看>>
nacos集群搭建
查看>>
Navicat for MySQL 查看BLOB字段内容
查看>>
Neo4j电影关系图Cypher
查看>>
Neo4j的安装与使用
查看>>
Neo4j(2):环境搭建
查看>>
Neo私链
查看>>
nessus快速安装使用指南(非常详细)零基础入门到精通,收藏这一篇就够了
查看>>